If you haven't already, go watch the video Mastering Dynamic Programming by Tech With Nikola! This tutorial is based off that.
We will look into three examples today, and gain some new insights by visualizing the call trees.
- Fibonacci
- Minimum Coins
- Longest common subsequence
Fibonacci
This one is tried and true! But not bad as a starter:
fn fib(n: i32) -> i32 {
if n <= 2 {
return 1;
}
fire::dbg!("return", fib(n - 1) + fib(n - 2))
}
What does the call tree of fib(5) look like?
  |
| Call tree of `fib(5)` |
To make it more efficient, we can use a "memo" to cache the function calls. There are multiple ways to do this, let's try using a static HashMap:
lazy_static::lazy_static! {
static ref MEMO: Mutex<HashMap<i32, i32>> = Mutex::new(HashMap::new());
}
fn fibm(n: i32) -> i32 {
if n <= 2 {
return 1;
}
{
let mut memo = MEMO.lock().unwrap();
if let Some(o) = memo.get(&n) {
return *o;
}
// we have to release the lock here
}
let res = fibm(n - 1) + fibm(n - 2);
let mut memo = MEMO.lock().unwrap();
memo.insert(n, res);
res
}
Now, what will the call tree look like?
  |
| Call tree of `fibm(5)` |
Nice! We can see that the fibm(n = 3) (9th node) returned early.
Here is one more comparison for fib(10).
  |
| Call tree of `fib(10)` |
  |
| Call tree of `fibm(10)` |
We can see that the memo helped reduce the number of nodes down from 111 to just 19!
Minimum Coins
Let's get to a slightly more interesting problem. According to Wikipedia, the change-making problem addresses the question of finding the minimum number of coins that add up to a given amount of money.
Example 1:
Given the coins { 1, 2 } (with unlimited number), how many coins do we need to make up to 5?
The answer is 3, with coins 1 + 2 + 2. Now, let's look at the standard recursive implementation:
fn min_coins(m: i32, coins: &[i32]) -> Option<usize> {
if m == 0 {
return Some(0);
}
let mut count: Option<usize> = None;
for coin in coins {
let next = m - coin;
if next < 0 {
continue;
}
count = match (count, min_coins(next, coins)) {
(Some(a), Some(b)) => Some(a.min(b + 1)),
(Some(a), None) => Some(a),
(None, Some(b)) => Some(b + 1),
(None, None) => None,
}
}
fire::dbg!("return", count)
}
The call tree for min_coins(13, &[1, 4, 5]):
  |
| Call tree of `min_coins(13, ..)` |
With memoization, we'd use a context specific HashMap:
fn min_coins_m(m: i32, coins: &[i32], memo: &mut HashMap<i32, Option<usize>>) -> Option<usize> {
if m == 0 {
return Some(0);
}
if let Some(c) = memo.get(&m) {
return *c;
}
let mut count: Option<usize> = None;
for coin in coins {
let next = m - coin;
if next < 0 {
continue;
}
count = match (count, min_coins_m(next, coins, memo)) {
(Some(a), Some(b)) => Some(a.min(b + 1)),
(Some(a), None) => Some(a),
(None, Some(b)) => Some(b + 1),
(None, None) => None,
}
}
memo.insert(m, count);
count
}
Now, the call tree is reduced down to just 28 nodes:
  |
| Call tree of `min_coins_m(13, ..)` |
Not bad, right?
Longest common subsequence
This is the most interesting and practical problem. The video uses it to implement a git diff algorithm which is pretty neat.
Here let's go straight into memoizing, because otherwise it would never return even for trivial test cases:
struct Memo {
memo: HashMap<(usize, usize), usize>,
}
fn lcs_impl<T: Copy + Eq>(left: &[T], right: &[T], state: &mut Memo) -> usize {
if left.is_empty() || right.is_empty() {
return 0;
}
fire::dbg!("(i, j)", (left.len() - 1, right.len() - 1));
if let Some(n) = state.memo.get(&(left.len() - 1, right.len() - 1)) {
return *n;
}
let n = if left[left.len() - 1] == right[right.len() - 1] {
1 + lcs_impl(&left[..left.len() - 1], &right[..right.len() - 1], state)
} else {
let leftn = lcs_impl(&left[..left.len() - 1], right, state);
let rightn = lcs_impl(left, &right[..right.len() - 1], state);
leftn.max(rightn)
};
state.memo.insert((left.len() - 1, right.len() - 1), n);
n
}
The .len() - 1 bits are pretty verbose, but if you look pass them, the code should be pretty understandable. The clever bit here is to use a HashMap with a tuple key instead of a 2D vector to save space!
But it's only half of the story. Because we still need to walk the path again to re-construct the common subsequence:
pub fn lcs<T: Copy + Eq>(left: &[T], right: &[T]) -> Vec<T> {
let mut state = Memo {
memo: Default::default(),
};
let length = lcs_impl(left, right, &mut state);
// reconstruct the common subsequence
let mut seq = Vec::new();
let (mut i, mut j) = (left.len() - 1, right.len() - 1);
while seq.len() < length {
if left[i] == right[j] {
seq.push(left[i]);
if seq.len() == length {
break;
}
i -= 1;
j -= 1;
} else {
if i > 0 && state.memo.get(&(i, j)).unwrap() == state.memo.get(&(i - 1, j)).unwrap() {
i -= 1;
} else {
j -= 1;
}
}
}
seq.reverse();
seq
}
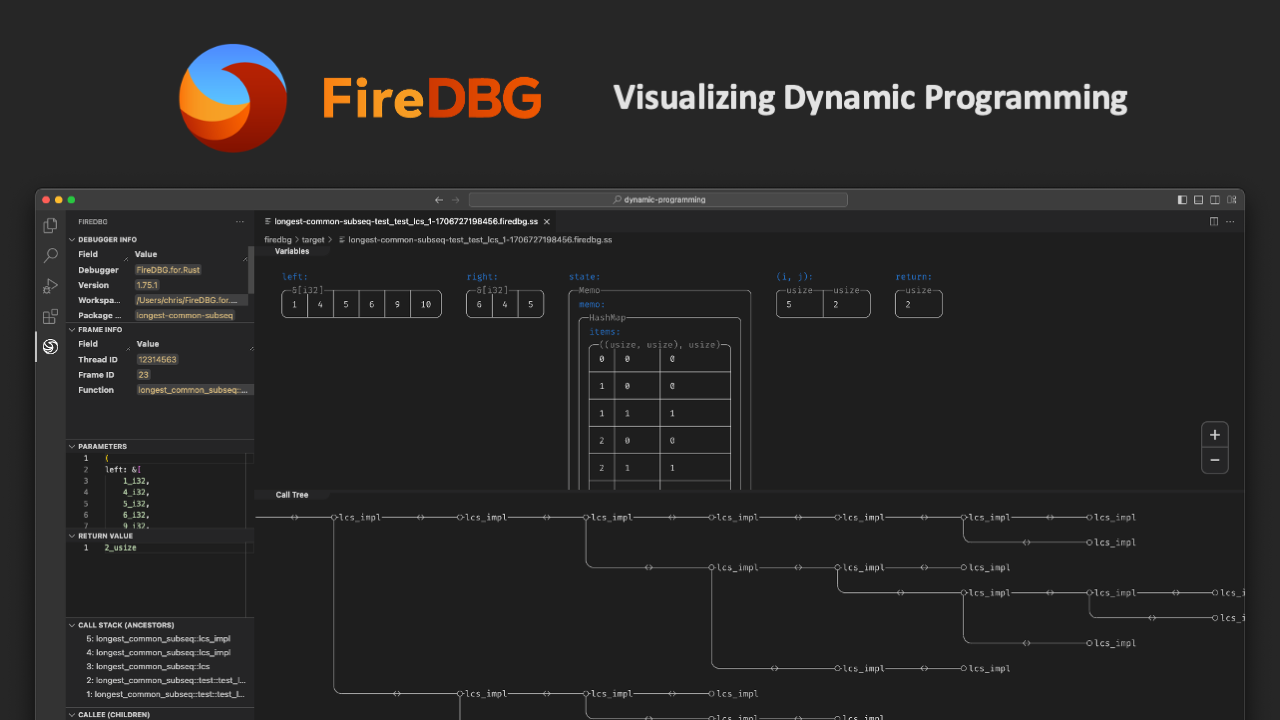
Here is the call tree for:
assert_eq!(
lcs(&[1, 4, 5, 6, 9, 10, 11], &[6, 4, 5, 9, 11]),
[4, 5, 9, 11]
);
  |
| Call tree of `lcs(..)` |
  |
| Memo of `lcs(..)` (last node) |
If we look into the memo of the last node, we can see that we only used 13 elements, instead of 8 x 6 = 48 as in the video (or pretty much every other tutorial), and that the call tree only has 35 nodes. So there is some trade-off between top-down vs bottom-up dynamic programming here.
Conclusion
I hope you learnt something today! FireDBG is your best companion in writing, debugging and analyzing algorithms. You don't have to install the Rust toolchain to interact with the call trees, as I have bundled them in the testbench with full source code here. You should be able to just open the dynamic-programming folder, install the VS Code extension and start playing.
Rustacean Sticker Pack 🦀
The Rustacean Sticker Pack is the perfect way to express your passion for Rust. Our stickers are made with a premium water-resistant vinyl with a unique matte finish. Stick them on your laptop, notebook, or any gadget to show off your love for Rust!
Moreover, all proceeds contributes directly to the ongoing development of SeaQL projects.
Sticker Pack Contents:
- Logo of SeaQL projects: SeaQL, SeaORM, SeaQuery, Seaography, FireDBG
- Mascot of SeaQL: Terres the Hermit Crab
- Mascot of Rust: Ferris the Crab
- The Rustacean word
Support SeaQL and get a Sticker Pack!
